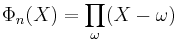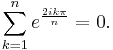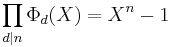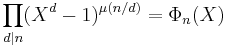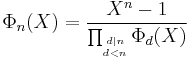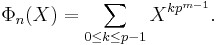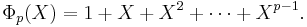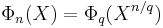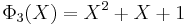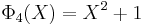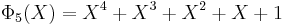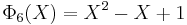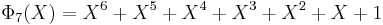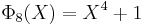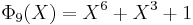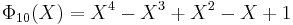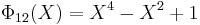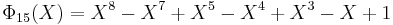Cyclotomic polynomial

In algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:

$\Phi_n(X) = \prod_\omega (X-\omega)\,$

where the product is over all nth primitive roots of unity ω in a field, i.e. all the complex numbers ω of order n.

1 Properties
2 List of the first cyclotomic polynomials
3 Applications
4 See also
5 References
6 External links

Properties

Let us set $\Phi_{1}(X)=X-1$ .

Fundamental tools

The degree of 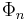$\Phi_n$ , or in other words the number of factors in its definition above, is φ(n), where φ is Euler's totient function.

The coefficients of 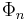$\Phi_n$ are integers, in other words, $\Phi_n(X)\in\mathbb{Z}[X].$ This can be seen elementarily by expressing the coefficients of the polynomials as elementary symmetric polynomials of the primitive roots, and to proceed inductively by using the relation:

$\sum_{k = 1}^n e ^{\frac{2ik\pi}{n}} = 0.$

The fundamental relation involving cyclotomic polynomials is

$\prod_{d\mid n}\Phi_d(X) = X^n - 1$

which amounts to the fact that each n-th root of unity is, for some divisor d of n, a primitive d-th root of unity.

The Möbius inversion formula yields the equivalent formulation:

$\prod_{d\mid n}(X^d-1)^{\mu(n/d)} = \Phi_n(X)$

where μ is the Möbius function.

From this fact, or alternatively, directy from the fact that the roots of a cyclotomic polynomial are the primitive roots of unity, we can calculate 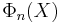$\Phi_{n}(X)$ by dividing 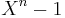$X^n-1$ by the cyclotomic polynomials of the proper divisors of n:

$\Phi_n(X)=\frac{X^{n}-1}{\prod_{\stackrel{d|n}{{}_{d<n}}}\Phi_{d}(X)}$

(Recall that $\Phi_{1}(X)=X-1$ . )

The polynomial 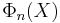$\Phi_n(X)$ is irreducible in the ring $\mathbb{Z}[X]$ . This result, due to Gauss, is not trivial.^[1] The case of prime n is easier to prove than the general case, thanks to Eisenstein's criterion.

Cyclotomic polynomials and arithmetic of integers

If n is a prime power, say p^m where p is prime, then

$\Phi_n(X) = \sum_{0\le k\le p-1}X^{kp^{m-1}}.$

In particular ( for m = 1)

$\Phi_p(X) = 1%2BX%2BX^2%2B\cdots%2BX^{p-1}.$

Any cyclotomic polynomial 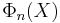$\Phi_n(X)$ has a simple expression in terms of 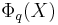$\Phi_q(X)$ where q is the radical of n:

$\Phi_n(X) = \Phi_q(X^{n/q})$

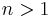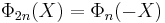If $n > 1$ is odd, then $\Phi_{2n}(X) = \Phi_n(-X)$ .

Integers appearing as coefficients

If n has at most two distinct odd prime factors, then Migotti showed that the coefficients of 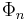$\Phi_n$ are all in the set {1, −1, 0}.^[2]

The first cyclotomic polynomial with 3 different odd prime factors is 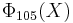$\Phi_{105}(X)$ and it has a coefficient −2 (see its expression below). The converse isn't true: 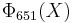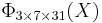$\Phi_{651}(X)$ = $\Phi_{3\times 7\times 31}(X)$ only has coefficients in {1, −1, 0}.

If n is a product of more odd different prime factors, the coefficients may increase to very high values. E.g., 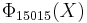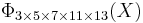$\Phi_{15015}(X)$ = $\Phi_{3\times 5\times 7\times 11\times 13}(X)$ has coefficients running from −22 to 22, 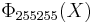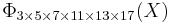$\Phi_{255255}(X)$ = $\Phi_{3\times 5\times 7\times 11\times 13\times 17}(X)$ , the smallest n with 6 different odd primes, has coefficients up to ±532.

List of the first cyclotomic polynomials

$~\Phi_1(X) = X-1$

$~\Phi_2(X) = X%2B1$

$~\Phi_3(X) = X^2 %2B X %2B 1$

$~\Phi_4(X) = X^2 %2B 1$

$~\Phi_5(X) = X^4 %2B X^3 %2B X^2 %2B X %2B1$

$~\Phi_6(X) = X^2 - X %2B 1$

$~\Phi_7(X) = X^6 %2B X^5 %2B X^4 %2B X^3 %2B X^2 %2B X %2B 1$

$~\Phi_8(X) = X^4 %2B 1$

$~\Phi_9(X) = X^6 %2B X^3 %2B 1$

$~\Phi_{10}(X) = X^4 - X^3 %2B X^2 - X %2B 1$

$~\Phi_{12}(X) = X^4 - X^2 %2B 1$

$~\Phi_{15}(X) = X^8 - X^7 %2B X^5 - X^4 %2B X^3 - X %2B 1$

Applications

Using the fact that 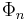$\Phi_n$ is irreducible, one can prove the infinitude of primes congruent to 1 modulo n,^[3] which is a special case of Dirichlet's theorem on arithmetic progressions.

References

^ Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
^ Isaacs, Martin (2009). Algebra: A Graduate Course. AMS Bookstore. p. 310. ISBN 9780821847992.
^ S. Shirali. Number Theory. Orient Blackswan, 2004. p. 67. ISBN 81-7371-454-1

External links

Sloane's A013594 : Smallest order of cyclotomic polynomial containing n or -n as a coefficient. The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.

zh-cn:分圆多项式